| Quantum Gravity | Jonathan Ainsley Bain |
| Before reading this chapter, study closely the previous chapter on Zeno and Planck |
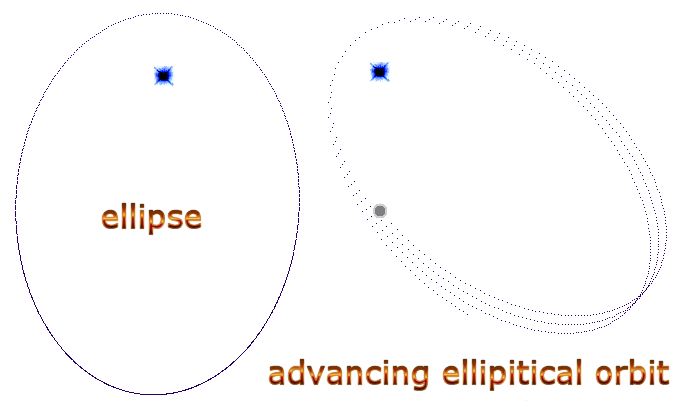
| The content of this chapter was realized the day before I was supposed to publish this book. Once these computations had been apprehended, they had to be written, despite the somewhat inconclusive results. This discussion is offered in the best spirit of adventure, incomplete for the positivist; because calculating the precise scale is just beyond immediate scope. I could discuss at length the difference between the ‘quantum nature of gravity’ and ‘calculations of individual instances of gravity quanta’. There are several other such slippery ideas, so the themes of ‘quantization’ and ‘gravity’ can intersect in different ways. But it seems that the argument becomes entangled at the notion of quantum time fitting into relative time. Quantum time is essential to all such calculation, and yet relative time has been measured. It is going to require something special to reconcile those two ideas. Nonetheless I have these thoughts, and I feel obliged to offer them (… albeit with hesitant trepidation at the consequences …) Einstein predicted that the orbit of Mercury was not an ellipse. He chose Mercury as the best example for two reasons. Firstly Mercury’s orbit is eccentric and thus less circular. And secondly, this eccentricity is closest to the sun.
Therefore the differences in velocities exhibited by Mercury at its
two extremities are most marked. As Mercury nears the sun, its velocity
increases due to its eccentricity, and its mass must then also increase
slightly. This would slow it down very minutely due to Einstein’s
formula. Thus the ellipse would exhibit a fluctuation. |
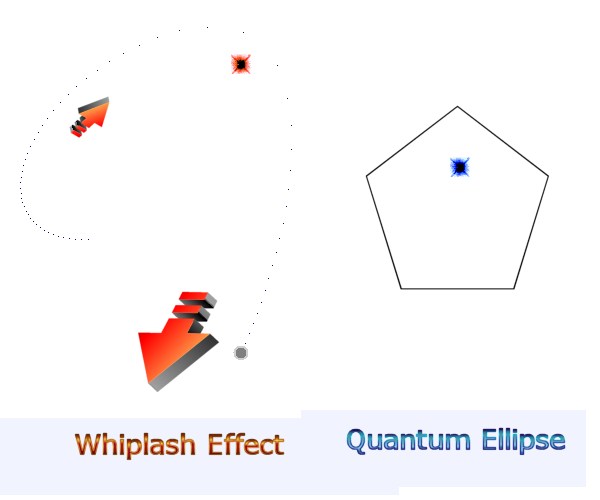
| One can see why Einstein insisted that orbits are not quite ellipses. But it is not nearly that simple. The phenomenon of perihelion drift was used to explain the observed fluctuations in orbits. The fluctuation was attributed to the gravitational force of the other planets in the solar system causing a sleight wobble to the orbit. The theory cannot be observed precisely as the amount varies so little with such huge calculations as to be negligible. Further theorizing attributed the phenomenon to space being curved. But I did not construct the “advancing elliptical orbit” (pictured above) using Einstein’s equations, though I could have. I did not change Newtonian gravity at all. Neither did I have to ‘curve space’ and thereby twist Newton in his grave into some other, painful contortion. The quantum nature of the universe constructed that orbit. All I had to do was increase the quanta used in the calculation by making the jumps between calculations, paradoxically larger. The phenomenon of orbits fluctuating then became observable purely for fundamentally Newtonian and natural arithmetic quantum reasons… The answer offered is that orbits are never quite ellipses! An ellipse requires that the body in motion return to its starting point. But! Because of quantum gravity, the orbit always returns to a point further advanced than a perfect ellipse suggests it should. The empirical proof is simply known as the ‘whiplash effect’ (AKA slingshot effect) whereby gravity can be used to increase a celestial voyager’s velocity. If all orbits were perfect ellipses, then the whiplash effect could not occur; as the celestial voyagers should always return to their starting points. Instead, such voyagers actually do travel away at great speed after such a close encounter with the planet and the quantum nature of gravity. The math to describe how quantum gravity distorts orbits away from the elliptical, and also describing the whiplash effect, was noticed when I attempted compute an orbit, and realized that the calculations have to be made step by step along quantum time. So when an orbital body moves close to a large body these effects can be exaggerated and the geometry simply observed. |
| Each calculation between points is a straight line, enhancing the effect. Ordinarily, if the dots are closer together then the effect is reduced significantly so that the orbit is almost an ellipse. Almost; but not quite. The intuition to this theory is based on constant observation of the whiplash effect in various computer models, and the realization that the whiplash effect and a perfect ellipse cannot occur in the same formula.
The whiplash effect is an extremely distorted orbit, and there is no
point where the distortion suddenly occurs. So; that distortion must
be there all the time; making orbits imperfect ellipses. The whiplash
is normally very small in near-circular orbits; and thus it is just
described as a minor fluctuation. The scale goes beyond measurements
smaller than pixels of course. This is where the uncertainty is. |
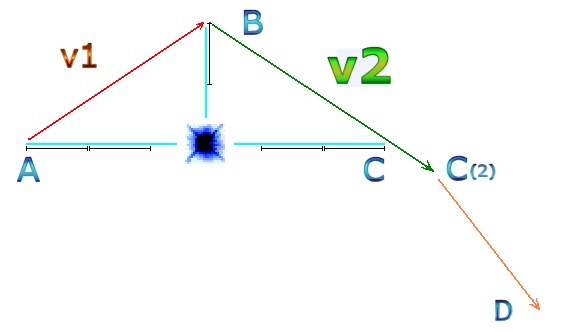
| In the image above, there are fewer calculations to the right of the star, because the velocity of the celestial voyager is faster after passing nearby to the star. (There are less time-jumps to the right of the star for a similar distance).
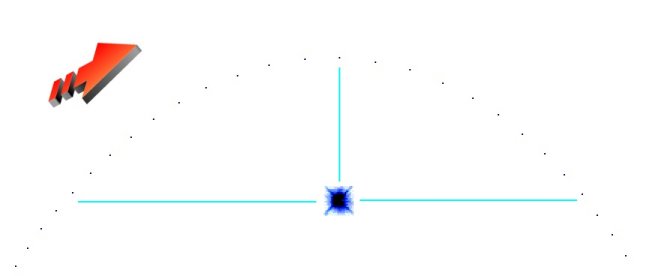
As we zoom down closer onto the quantum scale, we are essentially viewing
the top of what can only be described as a quantum ellipse. An ellipse
is symmetrical. So if we split a quantum ellipse in half down the middle,
there should be two equal halfs. But on the quantum level, the un-elliptical
nature of quantum gravity is even easier to see. |
| I’ll
call this the |
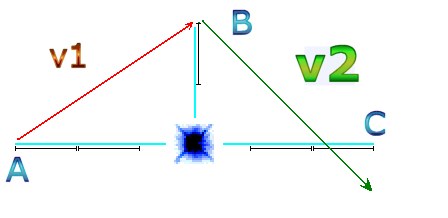 |
This is a schematic representation of two calculations of orbit under quantum gravity due to time being the constant measured unit (Quantum Time). The celestial voyager (moving A-B-C) gathers more velocity at point B than at point A. This is due to a higher force of gravity acting on point B, because point B is closer to the star. So, for velocity: v2 must be faster than v1. There is no other way to compute this in real time. If the orbit is perfectly elliptical then v2 would be equal to v1, which would result in the incorrect notion that the voyager would have an equal velocity at point A and point B. But! Because point B is much closer to the star, the stronger gravity accelerates it to a higher velocity than at point A. So v2 must be faster than v1. The only way v1 can be equal to v2 would be if points A, B and C are all the same distance from the star. If B is closest then v2 is fastest. Think about it. ABC can never be isosceles. Even if space is curved, all the phenomena within that curved space would curve with the curvature. Quantum gravity would still require orbits to not be elliptical. The calculations described here hold true regardless of curvature in space. Quantization of time demands it. If orbits were 100% elliptical then the voyager spacecraft would not have been able to leave the solar system using the calculations of the whiplash effect; because an ellipse always returns to its starting point and a whiplash orbit never does. An ellipse has no whiplash effect! The only way to solve the quantum gravity paradox is to conclude that orbits are not quite ellipses. Alternatively, if one tries to ignore the quantum nature of the universe, insisting that there are infinite points on a line, and thus infinite calculations, and not a series of quantum jumps, then one ends up with something similar to … …
an ultraviolet tortoise with infinite energy moving faster than Achilles
in in a perfect ellipse! |
| …
and yet the physics text book offers a similar problem with two other
solutions … |
|
|
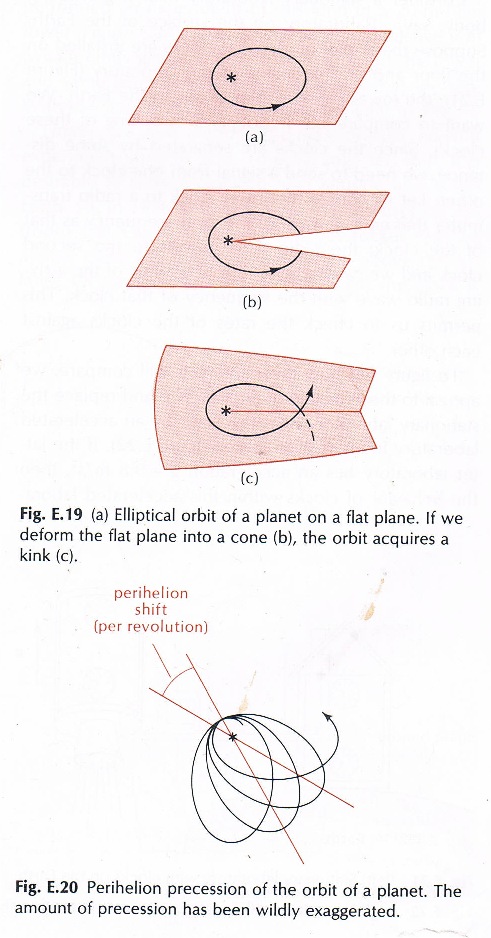
The
one solution suggests perihelion precession (distorted orbit) is caused
by other planets. |
| … and Einstein’s equations describe a similar orbital fluctuation too; as mentioned at the start of this chapter concerning Mercury’s orbit. But perihelion precession involves a distortion to the orbit that seemingly can only occur if the body slows down at the nearest point to the star.
Now quantum gravity causes a distortion to the orbit because the body
speeds up at the nearest position to the star! Perehelion
precession and the advancing ellipse are contradictory calculations
going in opposite directions to each other. That is why the precession
seems to require the opposite to the quantum gravity effect in the computed
geometry, which is thus a slight slowing down to get the orbit to precede. |
| Did Einstein predict that Mercury’s orbit would precede; but instead the measurement advanced? |
| Or did the orbit fluctuate both ways from one empirical observation to the next without the measurement reflecting any obvious uniformity? |
| How can Jupiter cause precession when half the time it is ahead of Earth and half the time it is behind Earth? |
| Surely Jupiter would cause advances or decreases depending on Jupiter’s position in relation to the Earth? |
| How does Einstein’s adjustment to mass (because of Relativity) generate a slower velocity when the whiplash effect causes a higher velocity? |
| Could quantum gravity counteract Einstein’s equations? |
| Is the Quantum Gravity Paradox (v2 being faster than v1) a computational rounding error; or is it the reason for the whiplash effect? |
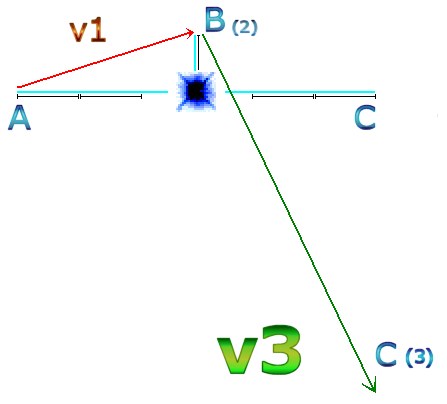
The scale of quantum gravitational effects may not be as much of a problem as initially anticipated. In the next calculation after C(2), quantum gravity causes a domino effect that compounds for each calculation. What this means, is that however many quantum leaps we consider, the whiplash still remains visible due to a knock on effect in the calculation. From point C(2) to point D and onwards the force of gravity is always less as gravity is less. Quantum gravity accumulates due to quantum time. |
| For
the reader who thinks this is still a rounding error, then nonetheless,
that ‘rounding error’ certainly still compounds like interest
does. Consider how it would look if B is moved closer to the star at
position B(2). The force of gravity is 9 times higher at point B(2)
than at point A as it is now one third the distance from the center
of gravity. So v3 takes an exaggerated quantum whiplash leap. |
| There
is just no way v3 will return to orbit, |
| Escape velocity is reached and the slingshot ensues. This can only happen because quantum gravity compounds for each successive calculation. Even if the quanta are much smaller than in the diagram, the effect must accumulate with each compounded calculation. The stronger the gravity, the denser the planet, the closer the orbital body gets to the center of gravity, the greater the whiplash effect will be, and this effect knocks on to every quanta after that. But the more acute that the angle of incidence is, the greater the slingshot is. A low fast circular orbit has no such effect even if gravity is high. The eccentricity of the orbit gives it acceleration, and this is where the quantum effect accumulates. And here is the bold claim: If the spacecraft fired its thrusters just before its closest point to the planet, then the amount of quantum accumulation can be maximized; and the slingshot enhanced considerably. It is quite a scenario to envision. The closer you get to the planet with the greatest acceleration at that closest point, the greater the gravity assist gets. A terrifically dangerous drama ensues, with spacecraft surfing quantum gravity for the best optimization of escape velocity. If the spacecraft gets too close to the atmosphere, it can either burn up due to friction, or be slowed down due to atmospheric drag. Some reports suggest the spacecraft can even bounce off the atmosphere like a stone bouncing off water when thrown at the correct angle; however, this phenomenon may be attributed to the slingshot effect. The closer that point B is to the star, (relative to A), the more pronounced the whiplash effect is. That’s why the whiplash is only a tiny fluctuation in an orbit like Mercury, and probably immeasurable for the Earth’s orbit which is almost circular. It may account for mere millimeters regarding the moons orbit. (I feel like apologizing to the publisher for the delay in writing. My excuse could be that space is curved, time slowed down, and that’s why the manuscript is a bit late. I’ll have to blame it all on quantum gravity.)
Curved space does not gel with me in the same way that the publisher
would be somewhat skeptical of curved time slowing down my writing.
The curvature of space (although real) seems to be a sophistic solution
for too many anomalies. Curving time would give the same answer computationally.
And fluctuations in time have been notably observed (or have they?)
Curved space still contains within it, normal straight-space geometry,
and curved space is only required when considering the universe as a
whole. There are quite a few variables competing for that illusive fluctuation
in Mercury’s orbit. Just when I thought the problem was looking utterly over-complicated, it suddenly gets simpler…
The many-body problem (from the text book quoted earlier) is a computational
problem that I had solved in 2008. Long before I realized it was a problem. |
| Many-body
Solution (Simply): Store all the potential momentums for each body in
a ‘holding matrix’ before even beginning to add them to
each or any of the existing positions. |
|
|