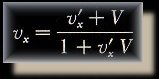| Relativity
Revised |
|
| Jonathan
Ainsley Bain 29 March 2014 Version 3 updated - 8 August 2015 |
|
| There
are several reasons why Einstein’s Special Theory of Relativity
is incorrect:
1)
The Dilation of Time Conundrum & Dilemma. |
|
The central method I am employing in this chapter is simply to test for internal logical consistency. The process whereby this ensues is to attempt to construct a real-time data-model of Relativity in Visual Basic 6. This is where most of the inconsistencies in Relativity become apparent. This is quite a lengthy article, so before I begin I would first like to make the two points that are the easiest to grasp: {A} Relativity proposes that space contracts as an object approaches the velocity of light. Such a contraction has never been observed. In fact many years after Relativity was first published, it was observed that space is expanding evenly in all directions. {B} The Michelson-Morley experiment can be explained by realizing that the medium through which light is moving, is itself simply moving with the Earth. {A} proves Relativity to be unempirical. {B} is the explanation that replaces Relativity. Perhaps before continuing, the reader may want to spend some time pondering these points carefully and methodically. It may be unwise to carry on reading until the reader fully grasps the implications of these two points. It is dogma to cling to a theory that has been proven to be completely at odds with empirical proof. Do not fall into the trap of assuming that something must be true because it has been accepted by many people of high status for a long time. Do not mistake the ability to recall a set of claims, with the ability to compute the logical connections (and indeed contradictions) between these claims. It is just not possible to program a real-time data model when the various formulae within that model are in contradiction to one another. This does not mean that my revision is necessarily correct. But the real-time data-model has certainly shown up the contradictions within Relativity. The data-model thus becomes a minimal benchmark for the internal logical consistency of any mathematical theory. |
|
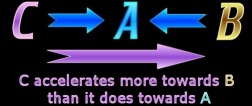
Two unmoving spaceships: A & B are the same distance from an observation point C. The observer at point C sends a signal in both directions which will reach A & B after the same amount of time. This signal thus starts both spaceships moving simultaneously. Both spaceships accelerate identically and reach the same high velocity on their way to point C. This velocity is close enough to the velocity of light so that they should apparently be significantly affected by time dilation according to the principles of Special Relativity. |
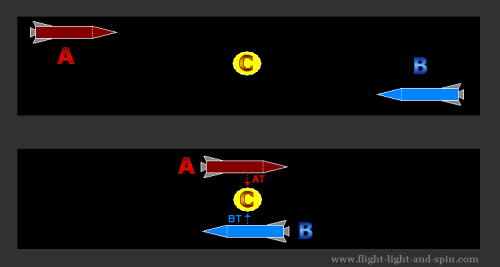 |
|
At the precise point that they pass by C, both spaceships send a signal which is the measurement of the time on their own clocks to reach point C. These signals are marked AT & BT in the second diagram. Both spaceships are in a state of perfect symmetry from the perspective of C. It is therefore clear regardless of the exact value of AT & BT, that these measurements of their respective times (including any time dilation) will be equal to one another at the point of passing C, from the observation point of C. Thus AT = BT when perceived from the observer at C. However the signals sent out are also both received by the other ship! So A receives the signal BT, and B receives AT. There will be a very small delay in the time that it takes the signals to pass between the ships. Seeing as the measurement is taken before the signal is sent (as they both symmetrically pass by point C) this will not affect the actual measurement, and thus the signals sent will be identical. Both
ships each will therefore be able to see that the times of their flight
are such that: This proves that time dilation due to relative velocity as specified in the Special Theory of Relativity can only be a logical and empirical impossibility!! Such a Principle as Time Dilation in the Special Theory of Relativity is self-contradictory. |
|
Download
this particular thought experiment for print purposes here: DILATION OF TIME conundrum.pdf or as an image file here: Time-dilation.gif You are more than welcome to use this for any teaching process. |
|
THE
DILATION OF TIME DILEMMA |
| The
dilation of time conundrum was previously published online
as the dilation of time dilemma. It is essentially the same
problem, but I repeat the original thought experiment here. Many people
could not comprehend the dilemma, which is why it was rephrased as the
conundrum. |
|
A and B are small bodies accelerating away from each other due to the force of gravity which is the result of the much larger yellow and blue stars.
From the perspective of A, the body B is accelerating away. Thus B should experience a time dilation relative to A. So, time for B is expected to slow down relative to A. And yet from the perspective of B, it is A that should experience time dilation! Clearly if both experience the time dilation, then time will be the same for both, and the result is that there is no time dilation. This is quite a problem. Both A and B cannot be suffering from the same degree of time dilation without there being no effective time dilation between them. Of course if we take the point of reference to be C, it looks like we solve the problem.
But both A and B are still accelerating away from each other without any effective time dilation. As we shall see later, the formula for time dilation is derived from the formula for space contraction and the formula for velocity reduction. So if we consider that there simply cannot be a time dilation between A and B, then how can there be a velocity reduction between them? The formulae for both time dilation and velocity reduction have the same mathematical origin. The tragic result of this is that without a velocity reduction, there can be no limit between them as regards the velocity of light! Of course it can be insisted that all the calculations regarding Relativity must be made according to the center point C. But this is in total violation of the principle at the core of Relativity: There is supposed to be no absolute fixed point of reference at all! This
shows that the Special Theory of Relativity is, at the least, incomplete;
and at the worst, fundamentally flawed. |
|
This problem further explains how the various premises that comprise Relativity are mutually exclusive to one another. Consider this straight line: Objects C & B are accelerating towards object A under the force of gravity.
Now,
according to Relativity, the adjustment made to the velocities would
therefore be different depending on which object it is accelerating
towards. The two measurements have a different nearness to the velocity
of light, so the Lorentz formulae will reduce velocity differently. So!
The change in velocity of object C
under the effects of Relativity would then be different in relation
to the two other objects. The result would be that object C
has a different position in relation to the other two objects! Once more, Relativity causes a blatant contradiction. Of course it will be countered that they are not in the same time, and space ‘contracts’ depending on relative positioning. But in order to compute this, we still need to measure such relations in an objective frame of reference. If two objects have ‘different times’, then those two times still stand in proportion to one another. We still must calculate such a relation objectively. The only way this can be done is to use an over-arching time frame. All other time frames would have to be in proportion to this. So the only way to compute relative time is to do so in proportion to an objective time. Now the contraction of space has never been observed, but even if it had, any such contraction would still be measured according to an objective frame of reference. How could we possibly measure any type of contraction, unless we said it was contracting in relation to something that was not contracting? If we say that our reference frame is also contracting, then it would be impossible to calculate it. Such a contraction could never be objective. It could only be illusionary. We commonly observe that a tree on the horizon is much smaller than the same tree up close. Our relative position makes it appear smaller. If we place a ruler next to the tree on the horizon, then the ruler itself appears smaller. But nobody can possibly agree that the tree itself has two different sizes depending on our relative position. I am not saying that Relativity is the identical to the tree on the horizon. What I am saying is that the objective frame of reference must be a premise before we can calculate what a relative observation will appear to be. Never mind that relative time is wholly at odds with Planck’s notion of quantum time. Any difference in ‘times’ still must be measured in relation to an objective frame of reference, in order to be measured at all. How can a quantum of time dilate without consisting of an even smaller quantum of time? (I will get back to this later). This is perhaps not making sense to those who hand-write exams on the material. They can always just resort back to the basic principles of Relativity, regardless of how mutually exclusive to one another they are; write them down, and feel that such constitutes ‘understanding’. The teacher grades the work, and if they have memorized ‘correctly’, then they get the grades – and this is considered ‘understanding.’ But it all becomes quite clear when one tries to compute 3 objects in real-time. The real-time computer algorithm cannot compute the incomputable. The positions of the objects in space, and their position in time must stand in proportion to one another objectively. The computer algorithm always gives contradicting mathematical data, and conflicting visual data, when we try and compute 3 objects under the principles of Relativity. Most of calculus is redundant when compared to the real-time algorithm. There is very little in calculus that cannot be calculated better, faster, and more accurately with a real-time algorithm. Any inconsistencies in premises will be shown up when trying to execute the program. The experienced programmer will realize these problems when trying to begin the construction of the algorithm with 3 objects or more. |
| (interlude) |
| If at this point, you are content that Relativity has fundamental errors in its calculations, you can skip through to Section 10 in Part 2 which begins to rectify the problem by dealing with the difference between a wave and a particle. If you really want to ‘cut to the chase’ – then skip to Section 14, which answers the crucial question: ‘Can we reduce added momentum whilst conserving momentum?’ These
web-pages consist of selected extracts of Chapter 27. You can download
the entire 36-page chapter here: Light
and Spin - Chapter XXVII (.pdf 3 mb). It is advisable to print it
out, so that your full concentration is on the article, and you are
not distracted by the computer. (It is also black text on a white background). If you still need more proof that Einstein’s Special Theory of Relativity is fundamentally flawed (or are just curious) then continue reading… |
| Firstly Relativity claims that all velocity is relative and that there is no difference between object B moving away from object A; or, object A moving away from object B. It also claims that there is no point in the universe that has zero velocity. This claim is due to the Michelson-Morley experiment (more on this later). Secondly, Relativity also claims that an object’s mass increases as its velocity increases according to the Lorentz transformation: |
| Now
it seems blatantly clear to me that these claims are logically at odds
with one another in such a way as to be mutually exclusive in purely
computational terms. How can we consider that velocity is relative and
there is no such thing as a fixed point of reference, and then at the
same time talk of an object being at rest by having ‘rest mass’?
But
let me take this further: Consider the scenario where you are located
at position A. Object
B is moving away from
you at some small velocity, and object C
is moving away from you at some much greater velocity. |
|
Now according to the notion that velocity
is relative, we could equally say that A
is moving away from C
at some great velocity or C
is moving away from A.
A
is also moving away from B
by some small velocity or B
is moving away from A.
According to this theory, it makes no difference which is moving away
from what, thus the arrows (above) are depicted going in either direction.
But the increase in the mass of A is a large amount relative to C but it is a small amount relative to B? So which one is it? Surely this is a contradiction of the highest order? We cannot be adding both increases in mass? For then we would have to increase mass enormously due to most objects receding from one another at ever increasing velocities due to the expansion of the universe. Somewhere there is a galaxy on the other side of the universe moving away from you at near the velocity of light, thus you are moving away from it, and thus your mass is now almost infinite. That is just not possible. (Of course we have no way of deciding which is at rest in the first place.) A potential answer to this dilemma could be that we need to allegedly add the sum of these velocities together before somehow applying the Lorentz transformation. But let me head this idea off at the pass. If this were true we would then have to add the velocities of all the particles in the universe together first, which are going to average zero. We would need to ignore the expansion of the universe to do this. The Lorentz transformation, at best negates itself, and at worst is just plain false as it will give every object in the universe almost infinite mass. Either way it will not compute. But
now consider this quote from Feynman (p. 88): |
 |
| So
because two objects are moving towards one another, Relativity gives
them an increase in mass due to their velocity. The mass is carried
over in such away that if these two objects collide, then their combined
mass is more than the sum of their masses before they started moving.
How
can that work? Do the atoms increase in mass, so that the atomic mass
is not constant? Or do extra atoms materialize to give added mass?
Considering that some atoms have undergone more velocity changes than
others over the history of the entire universe, it would be expected
that there should be quite vast discrepancies in the mass of atoms. But as I have already shown, the concept of relative mass breaks down for a much simpler reason. The formula clearly states that there is a phenomenon termed: ‘rest mass’. But! In Relativity there is no such thing as ‘rest’ because the objects are moving relative to each other. Relative mass fails empirically and also in terms of its own internal logic. |
| In the Ohanian textbook I find three references to photons having zero mass and two which claim that light must have mass, because it has energy. Feynman also seems to realize that if light has energy; and energy and mass are interchangeable, that light must then have mass (Feynman, p. 102). But most theory claims photons have no mass. Most readers should be familiar with the horrendous term ’wavicle’ (even my spellchecker does not like it) which has been used to describe the ‘dual nature of light’ which ‘sometimes behaves as a particle and sometimes as a wave’. The ‘dual’ nature of light is a blatant contradiction. What follows is Newton’s formula for calculating the total gravity between two objects. From Ohanian: |
| Now
the issue of gravitational lensing causes these two formulae to flatly
contradict one another. In the formula of Newton, if one of the bodies
has no mass, then either the ‘M’ or the ‘m’
is zero and there will be no force of gravity. So if the photon has
no mass then it is not subject to gravity!
But gravitational lensing is empirical proof that photons are affected by gravity! Hence the photon must have mass, or Newton is wrong? Seeing as though the laws of Newton have been used to predict the existence many celestial objects before they were seen, it seems that Relativity is the theory at fault! And yet, the Compton affect (Ohanian, p. 910) shows that photons impart momentum. The formula p = mv then proves that a photon must have mass or else the photon could not impart momentum. The momentum of the photon would be zero if its mass is zero. We can use p = mv to calculate the mass of the photon, which is its momentum divided by the velocity of light. In the second formula (above) called the Lorentz transformation if ‘v’ as equal to ‘c’ then the object is traveling at the velocity of light and mass becomes infinite. So now if the photon has some mass then that mass is infinite? Even if the photon has no mass, we still get a division by zero error! If v = c then the denominator in the latter formula is zero regardless of the mass. Many
theorists seem to prefer allowing Newton to spin in his grave rather
than Einstein. That is why it is more pervasive to read about a photon
having no mass, than it is to have people declare Einstein wrong. The
torturous concept of the wavicle tries to warp our minds into accepting
that these two ideas are not contrary, and the notion of ‘bent
space’ is bundled in to bully our brains into submission. |
|
I have already shown how Newton’s law divides by ‘r’ to the power 2 precisely because it is confined to 3d space in a previous chapter. Just to remind you: Any
process spread out at three times the distance covers nine times the
area. |
| Now
if space is bent (which I do believe to be true) then the law of gravity
will bend with it, and therefore nothing strictly existing within this
bent space will be affected by the bend!
Let me demonstrate the above idea in simpler terms. Draw a star with an ellipse orbiting it on a piece of paper, such that it complies with Newton’s law of gravity. Now if I bend or buckle the piece of paper, then the mathematical relationship between the star and the orbit will not change from a perspective confined to that piece of paper. Or if you prefer, use an orbit game with a bendable computer screen. Bending the screen does not affect the laws within the screen. Yes, space is bent. We can determine this because of the expanding universe. The only way that the most distant galaxies can be retreating at the fastest velocities is by realizing that the universe is expanding in all directions at the same time. The only way that the universe can be expanding in all directions at the same time is because it is a four-dimensional sphere. We can see this because of the popular balloon analogy. If we are positioned at one point on the surface of an expanding balloon then the points of the expanding balloon that are the most distant from us will expand away from us at the fastest velocity. So the shape of our universe can only be a four-dimensional expanding sphere. And the surface of any sphere is a bent curve. But if we draw a circle on that balloon and push a finger into it, to cause a dent, then the line of that circle may appear distorted from our perspective, but anyone confined to the surface would have their perspective also dented, and so would not notice the dent. Any law that is strictly confined to the surface bends with the surface. As I said in another chapter, to describe gravity as bent space makes mathematical sense. But the phrase ‘gravity is bent space’ is entirely different from ‘gravity and bent space’. If gravity is bent space then bent space is already accounted for and cannot be added a second time! If we consider gravity to be bent space, then the laws of Newton must still apply. If an object has no mass it will still not be affected by the bent nature of space. Of course the very notion that an object can have no mass I have already shown to be impossible. You can read more on gravitational lensing at this link: gravitational lensing |
| According to Relativity, as an object approaches the velocity of light, momentum that is added in purely Galilean (or Newtonian) terms has to undergo a transformation so that it only ever approaches the velocity of light and never reaches it. So if a starship is moving at half of the velocity of light and it fires a missile which is calculated to also move at half the velocity of light, the net result is that the missile only moves at 4/5ths the velocity of light. The following formula must be expressed with velocity in terms of ‘C’ (the velocity of light). Thus all the velocity values entered into this formula must be less than, or equal to one, expressed as a fraction of the velocity of light. From Ohanian: The new velocity is the sum of the two velocities divided by one plus their product. The formula for the ‘combination of velocities’ is derived from the two fallacies of contracted time and contracted space which are to follow in the next section. So go ahead and place some values into the formula and see how well it works. This really seems like a nice formula. I would not want to hurt it. And yet, if our starship is stationary and fires a missile, then that missile suffers from none of the effects of Relativity. If one of the velocities is zero then Relativity has no effect. Put that data in the formula and see for yourself. The problem here is that no missile just jumps to its intended velocity. It starts off slowly, and accelerates. So it is not really possible to just sum the velocities. We are in a very similar dilemma to Zeno’s Paradox here. (Click here for the chapter on Zeno's Paradox). We need to calculate every tiny increase in velocity with every microscopic adjustment over every quanta of time. If we do this, then the missile will have a different calculated velocity as to when we do not do it this way. If every split-second the missile is losing some of its added velocity according to this formula, then we have a problem, because if we do not use quantum time, then one of the velocities is zero and then we do not lose any potentially added velocity due to Relativity. The accelerating missile loses velocity whereas the instant missile does not. That is two different answers. If, for example we jump four times in periods of 0.1C we get a different answer to if we jump in two periods of 0.2C. Another example: According to the formula, if we firstly jump to 0.25C and then again another 0.25C, (to 0.5C) the second jump is contracted, the first is not. If we jump straight to 0.5C then there is no contraction at all. Quantum time is the only way to solve this. We cannot jump in large amounts, and the smaller we make quantum time, the smaller that first jump is going to be (the one that has no contraction). The margin of error is in proportion to how accurate quantum time is measured at. But if a photon comes into existence at the velocity of light then the formula adds up to one, which is quite fine as that is the velocity of light. I have called this a ‘mystery’ rather than ‘catastrophe’ as the formula works. The formula is merely inaccurate, and not ‘wrong’. But then again, as we shall see, the light-barrier is not quite so sacred either! But quantum-time is an imperative. |
| Apparently, Relativity requires us to contract space, and also to slow down time when the velocity gets extremely high. The ’Lorentz Transformations’ are the calculations which are derived form the formula used for the summing of velocities. Or the summing of velocities can be derived from the Lorentz transformations if you prefer (Feynman p. 80-81). The following formulae are from Ohanian (p. 430-431): As you can see, the x is the contraction of space, and the t is the contraction of time. Now one of the mistakes they made is that these two formulae are derived from the contraction of velocity. Feynman takes us through these calculations (Feynman, p. 80-81). So, if we calculate that added velocity contracts, then these two formulae have already been applied! But poor old Lorentz never used these formulae in this way himself at all! Tangled indeed! But there are even more contradictions with contracting time and space than this. The problem becomes evident when we try and calculate more than two particles with varying velocities. This is similar to the relative-mass-catastrophe, in that we are expected to contract space and time differently relative to different particles. Never mind the time issue, just consider the space issue for now. |
| If a block of space contracts differently relative to every particle in the universe, then the entire concept of space becomes increasingly contracted with the more particles we take into account. In the following diagram four objects are depicted: G, R, B, P, as well as an empty unmoving space labeled: ‘Y’. The objects are moving away from ‘Y’ as the arrows of the relevant colors show. The numbers 1,2,3,4 situated below Y represent the contractions in space that Y will experience in relation to the four pairs of objects moving away from it. Contraction 1 is the contraction between R and B, 2 is the contraction between G and P, etc. So any object that may be in position Y is going to be increasingly contracted with the more objects we add either side of it. If we consider that G and P are galaxies on the edge of the perception of the best radio telescopes, then their velocities are going to be quite close to the velocity of light, so contraction 2 at position Y is going to be most extreme! Can you see the problems yet? (Do you feel particularly contracted?) Seeing as though every point at a far distance from us is moving away from us at velocities increasingly approaching the velocity of light, and all these particles have contractions, then we should have all contracted into such a narrow bit of space that we should have all but disappeared by now. Of course contracted space makes no sense for other reasons. One problem being that empirical observations show that due to the red shift or Doppler affect, the universe is not contracting, but it is in fact expanding... |
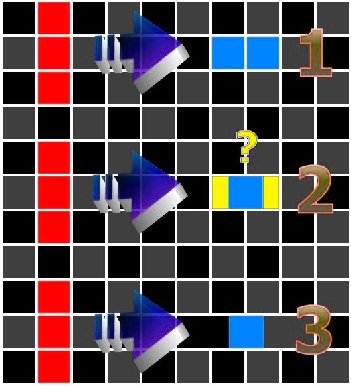
| Consider
four objects. At time=3 the Green object is in the Yellow square, whereas the Red object has moved one square to the right of that. |
 |
| According to Relativity, the space between the Red and Blue is contracted more than the space between Green and Purple, simply because Red is moving faster than Green. So when the Green moves into the Yellow block, it is moving into contracted Red -Blue space. But the contracted Green-Purple space is contracted differently to the Red -Blue space as the objects are traveling at different velocities and in different directions. And yet they are both expected to contract that same block with different contractions at the same time. So we are left with two contradictory calculations to make in the same time and place, both of which cannot be true. If we try and sum both those contractions, then we have to sum up all such contractions, and the result of this has already been shown to be illogical in the previous section. The nature of space being contracted defies the a priori concept of logic itself. Relativity asks us to imagine a dream-world, where a position in space is not the same position in space that it is. Such a concept as ‘this point in space’ can freely defy itself as if it were an apparition of Xanadu! The yellow block is where it is, and it is also elsewhere, at the same time as not actually being where it should be. This defies any attempt at objective calculation. Contracted space is illogical as it requires the premise of fixed space to begin with. So the conclusion to the calculation is at odds with the assumption that the conclusion is built on. It’s like trying to pick yourself up by your own bootstraps. Any distortions can only be measured by comparing those distortions to that which is fixed. When we alter an object’s position in space (or time), we can only do so in terms of reference to undistorted space (or time). So individual ‘contractions’ can only be a change in velocity through fixed space and fixed time. Even if we contract space and time regardless of the complexity, we still have to measure those contractions relative to that which is not contracted. Then all we have actually done is alter the velocity! It makes no sense to alter space or time, only velocity can change. We can try the notion of saying that each contraction in space only applies to each pair of particles. If we try and say that, then the yellow square contracts differently for each interaction. But that makes no sense because then the notion of space ceases to exist. ‘So’, says the devil on my shoulder, ‘space does not exist, so what?’ Well, if it does not exist then how can they say it has been contracted? In Visual Basic 6, we can actually give each particle its own event timer. So that the rate at which each of those objects moves is not only due to the number of pixels it moves (velocity). But the movement is also due to the speed at which we do each calculation. These speeds can differ for each object, and the speed of each event timer can be altered up or down as we want them to. So contracted time is computable. But it makes no difference. Those two timers still stand in proportion to one another. Conceptually: If we divide the speed of the timer’s calculation (time) by two, it gives the same result as if we divide the number of pixels moved (velocity) by two. ‘Slowing time’ is just another way of slowing velocity. ‘Contracting space’ is the same calculation. At least as far as two objects on their own are concerned, the result is conceptually the same as regards space. More than two objects in contracted space cause the problems already outlined. Space is spread out in universal terms, whereas time can be calculated in local terms. What happens to the space in between the two objects if the space is contracted? What about a stationary object that happens to be three-quarters of the way between two objects? Does its movement change now because that space is contracting? If so then it is not a stationary object at all! But we have already defined it as stationary? So that is a contradiction in terms! It is tempting to now suggest that the expanding universe may also fall foul in the same manner, but not so. The expansion of the universe takes place evenly over time. That can be calculated. Whereas these contradictory contractions here depicted take place differently for different pairs of objects within a single iota of time. We can stretch a piece of paper or calculations on a computer screen without any contradiction. But we cannot stretch it in contrary directions at the same time. We cannot stretch it and contract it simultaneously depending on which objects we are calculating. That would be asking us to do opposing calculations. We can try sum up the contrary contractions and expansions in a pre-calculated matrix, (in the way I solved the many-body-problem) but then we end up with a universe which should be contracting in an extreme fashion. Yet the universe is observed to be expanding! And because it is this expansion itself that results in the largest extremities of velocity; Relativity stands in stark contradiction to the observed universe, most especially when we try and apply it to every particle in the expanding universe simultaneously. Now I have said that we can stretch space without contradiction, but earlier I showed that our calculations for gravity were unaffected by stretching space. Whether it is light or gravity or anything else, that that is being calculated, the inverse of the square phenomenon is rigidly confined to the three-dimensional space within which it exists. Any phenomenon that decreases by the inverse of the square is perfectly spread out in three-dimensional space. The diagram from earlier should make this clear. The law of gravity is confined to three-dimensional space, but the geometry of space itself is four-dimensional. That is why we can expand the universe in four dimensions, but not affect the three-dimensional law of gravity when doing so. I read two ways in which it was postulated that space is said to contract. The one outlined above is a result of a direct application of the formula via Feynman. The more pervasive interpretation is that it is not space that is contracted, but instead just the object moving that somehow shrinks. But there is no way that the formula distinguishes between the object itself and the space it is in! I assume that this other interpretation of merely the object contracting was fudged in order to compensate for illogical conclusions similar to those outlined here previously. But how can the object contract, and not the space it is in? |
|
|
| A
Blue object is moving
away from a Red object
(1). If only the Blue
object (and not space itself) contracts then what happens to the fractions
of space (2) colored Yellow?
The only logical result (3) would be that the surrounding space expands
to fill the gap. This is contrary to the formula stating that space
contracts!
Of course what happens to an object moving vertically past (3) can only be incomputable. So even if we ignore the fact that it is space which is supposed to contract and fudge it so that just the object contracts; then we still end up with a contradiction in terms as the space next to it then expands to fill the gap. The internal logic required to construct a computer algorithm will suffer no such ideas to persist. Never mind that nowhere in the formula can we ascertain any such difference between the space itself and the specific object at all! |
| Many studies have been made of these famous experiments. I do not wish to repeat what others have said on the topic. Einstein rejected the results as they seemed to indicate that wave patterns were being transmitted faster than the velocity of light. I have read the original documents some twenty years ago and was satisfied then that they demonstrated a signal being transmitted faster than the velocity of light; albeit on a scale that was not at all useful for any commercial purpose. The distance transmitted was far too small to create a faster-than-light telephone. But it is just worth mentioning that there is empirical evidence that proves Einstein’s theory on Relativity is (at the least) empirically inaccurate. |
| <
top of screen > |