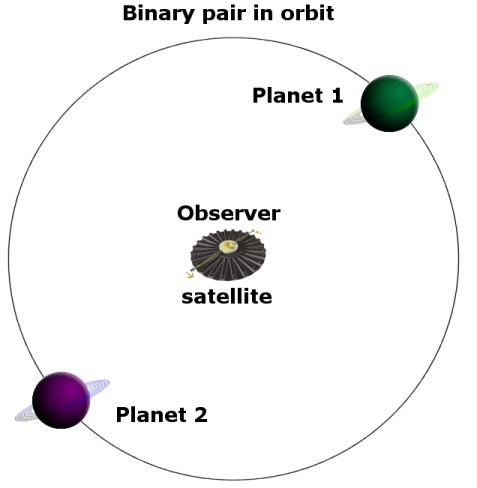
| Absolute & Relative Velocity, Orbits and Rotation It is quite clear and widely accepted that the rotation of a body around its own axis must be measured in absolute terms, and not relative terms (Feynman p.76). We can feel the effects of the centrifugal force quite markedly, and so we know that if a satellite in deep space is rotating, then astronauts will stick to the inner walls (simulating gravity). And if it is not rotating they will float in zero gravity. They will also be able to observe their rotation when they see the ‘fixed’ stars ‘moving’ past their window. The centrifugal force and the movement of the window past the stars will always coincide, absolutely. This is how we know that axial rotation is not a relative phenomenon. It is certainly absolute. Now consider any perfectly balanced binary pair of stars (or planets). In this example they have the same mass – and their orbit is not elliptical – it is as perfectly circular as possible. If we carefully consider this hypothetical pair in purely relativistic terms then we can only reach the strange conclusion that they have in effect no velocity relative to one another – because the distance between them is constant relative to one another. But if they have no velocity relative to each another, then there would be mutual attraction from gravity – and they would accelerate towards one another and then collide! I have labelled
this concept It is only when we consider a binary pair to be moving compared to the ‘fixed’ stars – or when compared to a barycenter (midpoint) – that gravity is counteracted by that orbital motion. The binary stars are now able to maintain a constant distance from one another as binary orbits are supposed to. Their absolute orbital velocity is now perfectly balancing the gravity between them. And the idea of BAOBAB subverts the core concept of Relativity so clearly, so clinically, that I can hardly wait in sheer mirth to hear the variety of sophistry that the compulsive Relativists will try and counter it with. But we need to follow BAOBAB further. We have the widely accepted proof that the Earth’s spin on its axis – being a rotation – is thus absolute and not Relative. So let us consider a satellite in a geosynchronous orbit – so that it orbits the Earth in exactly one day. This satellite is thus always directly above the same point on the surface of the rotating Earth, and it is also always the same distance from that point. So surely it makes sense to suggest that this satellite is moving in absolute velocity and not Relative velocity? Well the Relativists would certainly not agree. But in what critical sense are those two movements fundamentally different? What about the various points between the satellite and the surface of the Earth? Where are we supposed to draw that hypothetical line between Relative and absolute? We
can then also place an observer satellite precisely at the barycenter
(midpoint) between a pair of planets in a binary orbit. The satellite
has a constant rotation on its axis exactly equal to the time it
takes the binary pair to orbit one another. We have the same resultant
angular velocity for both the binary pair and for the axial rotation
of the satellite – when compared to the fixed stars –
or when comparing both these to the midpoint (barycenter). |
||
|
If the binary pair stops orbiting each other (when compared to the
fixed stars) they will attract one another because of their gravity
and eventually squash the satellite between them. By the same token,
if the satellite stops rotating compared to the fixed stars, the astronauts
in the satellite will experience weightlessness before they get squashed
(by the non-orbiting binary pair).
It is abundantly clear that if we only consider their orbit in purely Relative terms as regards one another – then there is no Relative velocity between them – and thus nothing to stop gravity pulling them together. The midpoint is a fundamentally necessary construct to the binary orbit, such that it is logically linked to the fixed stars in precisely the same absolute manner that a rotation is. So the midpoint is actually a fundamentally necessary third positional feature of a binary orbit. Thus
it must be concluded that the orbital rotation of the binary pair
is also only measurable in absolute terms. The Relativists will,
of course, just choose to disagree (because they are Relativists). |
||
| This is an extract summary of Chapter XXX of the book: Flight Light and Spin Download page for relativity simulation: algorithm orbit-gravity-sim-12.exe The full chapter can be downloaded here: Sum-Theory.pdf (5.5 mb, 57 pages, this pdf file is too big for chrome, use firefox) List of: abbreviated short articles . . |
|||||