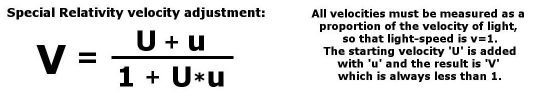| Relativity and Mercury's orbit The easiest way to assess the accuracy of the orbits of the planets in the evolutionary algorithm OGS12 (orbit-gravity-sim-12.exe) is to observe Scenario [18] which shows the orbit of Mercury according to Newtonian gravity at a time-scale of 1:10 000. The user can freely download the algorithm and observe all this data evolving in real-time. The error-margin at this time-scale is 1 part in 40 million millions or 177mm after 20 orbits. That error-margin of 177mm is the difference in the distance from Mercury to the Sun after those 20 orbits at aphelion (maximum distance.) Next
we select Scenario [5]
which alters the orbit of Mercury by adding the principles of Special
Relativity, such that accelerations towards the velocity of light
are reduced away from the expected Newtonian result using the following
formula: |
||
| So
we can clearly see that Special Relativity results in a reduction
in velocity when compared to Newton’s laws. The net result is
that when the orbit is at its nearest, Mercury moves closer to the
Sun at a rate of 832 meters per orbit. Whereas at it’s furthest,
Mercury spirals inwards towards the Sun at a rate 1.92km per orbit
as a result of this formula from Special Relativity.
. |
||
| Now
the knee-jerk response from so many people is that this amount is
counteracted by ‘other parts of Relativity’. So Scenario
[20] demonstrates the effect of General Relativity
on Mercury’s orbit, and Scenario
[21] combines both Special and General Relativity.
However,
General Relativity results in the nearest distance (perihelion)
moving outwards at a rate of about 35 meters per orbit, and the
outer distance (aphelion) moving outwards at about 50 meters per
orbit. Compare the data: |
||
|
|
||
This is an extract summary of Chapter XXX of the book: Flight Light and Spin Download page for relativity simulation: algorithm orbit-gravity-sim-12.exe The full chapter can be downloaded here: Sum-Theory.pdf (5.5 mb, 57 pages, this pdf file is too big for chrome, use firefox) List of: abbreviated short articles . |
|||||