The algorithm orbit-gravity-sim-15.exe (OGS15) computes precise gravitational effects that the various planetary bodies have on one another within the solar system. It is an entirely evolutionary n-body-gravity algorithm, which operates according to Newtonian-Planck gravity in 3D space. We improve on Kepler's singular body ellipse, by using the formula from Newton of g=Gm/r^2, in conjunction with quantum-time from Planck. Of course with the interacting gravity fields of 3 or more bodies in 3D space, the resultant shape of the orbits now deviate away from being purely elliptical.

For Kepler and Newton time was infinitely divisible, but for Planck, time itself could not be divided into units smaller than 5 x 10^-44 seconds: Distinct jumps in quanta of time. And it is paradoxically within these indivisible moments of time that we can compute the interacting gravity fields of multiple bodies (the n-body problem, or many-body problem). Quantum-time is thus the essential key to quantum-gravity.

The primary finding of this algorithm OGS15 (orbit-gravity-sim-15.exe) is that the phenomenon of Perihelion Precession is an emergent property of Newtonian-Planck gravity. So the orbital extremities of each planet rotate around the Sun in the same direction that the orbits themselves rotate, purely due to the gravity of the other planets. Beyond Perihelion Precession there is some other factor influencing the movements of the planets beyond Newtonian gravity that results in the quite different phenomenon of Precession of the Equinox. (More on that much later).

The algorithm is free here: Download
Help files on how it works: Orrery
The most essential parts of the source code freely available:
How to Build N-body-gravity Algorithm

However !

The amount of Perihelion Precession that has historically been claimed to be observed, is said to be greater than that which has historically been calculated using Newton's formula for the classical example of Mercury's orbit. But the manner in which Newton's laws are calculated for 3 or more bodies is not nearly as certain as it is for Kepler's simple ellipse. Mostly this is because all other such Newtonian n-body models fail to directly account for how the Z-axis dilutes the gravitational effects of the other planets.

Inclusion of the Z-axis in the algorithm specifically alters the Perihelion Precession of Mercury's orbit, by as much as 13%. Thus, historical and contemporary theory has wrongly calculated the Newtonian effect on Perihelion Precession with an error greater than the amount that they attribute to Einstein's Relativity.

In addition to this, the selection of a particular starting orbit for Mercury can vary the Perihelion Precession by amounts more than that attributed to Einstein's Relativity. The Relativists claim that their theory accounts for +43 arc-seconds per century of Perihelion Precession for Mercury, but individual orbits of Mercury have variant deviations to the perihelion, ranging from a recession of less than -40 arc-seconds per century to a precession over +80 arc-seconds per century between pairs of orbits. Changing the starting orbit or sample size can thus easily more than account for the amounts attributed to Relativity.

So their are at least two quite different basic flaws in traditional methodology which result in error-margins in total that are 3x larger than the amount traditionally attributed to Einstein's calculations.

The size of the sample can easily alter the Perihelion Precession to amounts beyond those attributed by Einstein's theories. The unit of measurement for Perihelion Precession is measured as an angle in arc-seconds over an entire century; which is the typical sample size used by less detailed analysis than this one. I frequently calculate samples of many thousands of years with a high level of detail, as will be demonstrated.

Moreover, the observations and the various accounts of n-body-gravity theory all differ, depending where you read. The actual claim of what Newton's theory should apparently predict and the observations both often differ by a logarithmic factor too. So the essential questions become:

1) Can the rotation of the orbital extremities of the planets around the Sun (Perihelion Precession) be entirely explained by Newton's paradigm, and if not, what can account for the difference?

2) Is their any consistent causal factor beyond Newtonian gravity in the celestial dynamics of planetary bodies in the solar system?

The short-answer to the second question here is: 'Yes!'

But we need to look at the given hard data to lay the foundation for the answer to the first question, being: 'no'...

There are claims that the amount of Perihelion Precession is 10 times less than what is depicted by utexas.edu (above). Mr Ohanian (below) gives a very picturesque description, but look closely to compare these two quotes for the Earth.

We simply cannot take university issue text at face value. There are also widely published numbers which are 10 times more than the utexas.edu table. And there is discrepancy as to what the actual difference is between the observed and the theoretical amounts too!

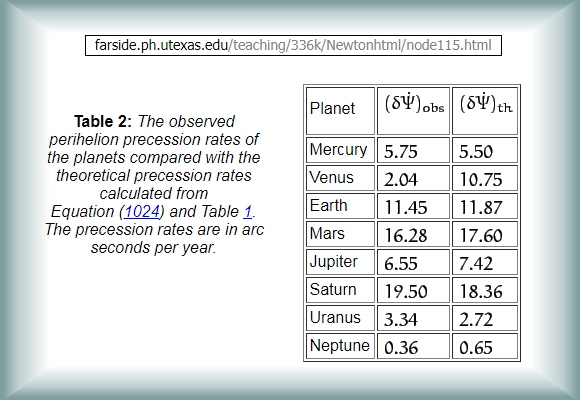
So which is it? Is observation of Perihelion Precession for Mercury 5600 or 575 or 550 arc-seconds per century? Is the discrepancy between observed and theoretical 43 or 25? And what accounts for those differences, precisely?

The only way to properly resolve these questions is to assume a strict logical-positivist methodology. This being to take no theoretical calculations for granted, and do all the sums from scratch oneself - and then compare the results to the various observational claims.

Well even my first approximation model in 2D (orbit-gravity-sim-13.exe or OGS13) shows that Mercury's Perihelion Precession is somewhere in the region of 547 (+-12) arc-seconds per century due to Newton's law. So it seems that the 5600 per century is wrong. But is it? The details are quite intricate. Regardless of which side we take, a sound methodology includes the careful consideration as to how the other side managed to get such a large error, or else its just a case of who cares to belligerate the most vociferously.

All my answers offer a transparent and repeatable methodology devoid of jargon and arcane symbols.

It is quite bemusing to read the phrase in the previous quote from Riverside that it is a 'fact that the Earth is not an inertial reference frame'! The moon certainly has not been informed of this 'fact' as her orbit is using the reference-frame of the Earth, and is also being carried along by the Earth's gravity which is a side-effect of the Earth having mass and thus inertia. The famous Michelson-Morley experiment and the 'twins paradox' all classically explain Einstein's Relativity by using the Earth as a reference frame!

So why are Riverside claiming the Earth is not an inertial reference frame?
The mis-representation from Riverside needs to be precisely understood on its own terms.
To be fair, their point actually does have some abstract merit, although their choice of wording shows that they have not fully appreciated nor understood their own statement. It has all the features of regurgitated-examination-based-theoretical-abbreviation.

Their confusing comment as to what qualifies as a valid inertial reference frame arises because the Earth and Moon orbit their common barycenter - and that barycenter is a more accurate reference frame than the Earth alone. But the Earth-moon barycenter can only be determined by considering each of their gravity from the source of its own inertial reference frame; then combining the two reference frames for a more accurate sum. So it would be correct to say that 'the Earth is not a complete reference frame'. It certainly is very much a valid and essential frame of reference for inertia and gravity in a genuine n-body solution.

When considering a satellite in orbit around the Earth, the Earth-Moon barycenter is more accurate than the Earth's reference frame alone, because the Moon will pull the satellite away from the Earth by a small amount. But when you jump up in the air, the Moon's tidal alteration to your jump is practically worthless, and the only meaningful frame of reference is the Earth.

But if we want to be obsessively accurate, then the only valid reference frame is the gravitational barycenter of the entire Universe. My algorithms always use the barycenter of the solar system as its essential point of reference. But this can only be calculated as a sum of all the reference frames of the Sun and planets. So the Earth certainly is an inertial reference frame. But its all just a matter of accuracy as to how useful it is to use it on its own.

In the Newtonian paradigm, any reference frame is equally valid so long as we take into account all the other significantly massive bodies. In fact any theoretical physics should hold to the principle that 'the laws of physics must be the same in all (and any) reference frames'.

But as we saw in the previous chapters, holding the formulae of Relativity to be the same in all reference frames, gives numerical results that differ between those reference frames!

Still, it all gets far murkier than this...

<— Page Back — Start Page — Next Page —>