Neptune's Orbit Perihelion and Aphelion

Its not easy to determine Neptune's Perihelion Precession for numerous reasons. The most astounding being that we need to observe the difference between two perihelions. Nobody could have observed such an event, because Neptune has not passed its point of perihelion twice since it was discovered. Neither has it passed its point of aphelion twice in this time. And yet there are commonly regurgitated accounts that Neptune's Perihelion Precession has been 'observed'.

But even then, there is not consensus as to when Neptune's perihelion is, in broadest terms. The angular difference between the following two depictions, I have measured as being about 45 degrees. Compare the perihelions and aphelions where the: ? (red question-mark) is situated in these virtual solar system models.


If you compare the positions of Saturn and Jupiter at the selected date above of 2020/1/1, there is a good approximate agreement. But the position of Neptune itself differs radically. Astronoo.com has Neptune ahead of the aphelion of Uranus, whereas in-the-sky.org has Neptune behind this position (orbital rotation is anti-clockwise). Before you decide who is 'right' and who is 'wrong' - read the rest of this article carefully. The method of logical positivism is to assume nothing, and prove everything.

But the disagreement of Neptune's actual position is about 7.2 degrees. Which is kinda tragic. But it is likely that one them made that error for reasons similar to that within the difficulty of establishing its perihelion.

Now the claimed 'observation' of the Perihelion Precession of Neptune is said to be 0.36 arc seconds per Earth-year (see Introduction). So from 1876 to 2042, the Relativists 'observed' Neptune's perihelion move 0.0165 degrees. Sure they did; after all, being Relativists they can time-travel through worm-holes into the year 2042 and 'observe' Neptune's next perihelion. Then back *SWOOSH* though the wormhole and let us know how much Neptune's perihelion has been observed to advance.

But really, now.


The 3D-n-body-gravity algorithm OGS15 shows that Neptune's perihelion and aphelion both average out after about every 8 orbital pairs, with about 7 successive preceding-orbits followed by a very large receding-orbit. But not precisely. The graph above is Scenario [28] of OGS15 algorithm.

.

After 24 orbital pairs from 1876 AD to 5826 AD the perihelion yielded an average movement of:

+2.09   as/Ey.

After 24 orbital pairs from 1803 AD to 5753 AD the aphelion yielded an average movement of:

-1.9   as/Ey.

.

It is thus not meaningful to give an estimate as to whether the movement of the major axis is overall positive or negative in these time frames. The error-margin within the computation is 0.16 as/Ey.

The best explanation for the strange data above is that Neptune's orbit will be somewhat in the shape of a kidney-bean for the next few millennia.


Neptune is the same as the other planets, in that we must also notice the aphelion movements are more orderly than perihelion are.

The Aphelion Recession of Neptune yields an average of: -1.1 arc-seconds per Earth year for that first cycle of 8 orbital pairs.

The Perihelion Precession of Neptune yields an average of +4.6 as/Ey for the same 8 orbital pairs. (Error-margin of +-0.47 as/Ey within these computations.)

Scenario [28] of the OGS15 algorithm (aphelion variation) iterated -1.1 as/Ey from 1803 AD to 3120 AD representing a cycle for 8 orbital pairs of 1317 years as it appears in the graph above. The vital point being that the aphelion from 1803 to 1959 had receded by more than -18 full degrees. That is contrary to all expected models. Now it should be clear as to why everybody is so confused as to what Neptune's orbit is  doing. Lets just look at the graphic of Scenario [28] where we can visibly see those variations to the aphelion.


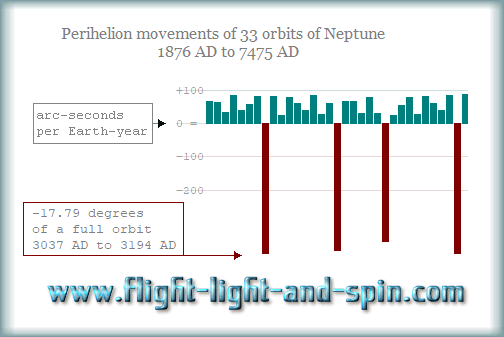
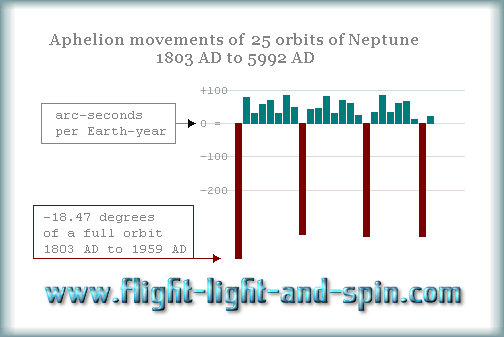
Its vital to see that because we are comparing 8 movements between pairs of aphelion, we are calculating the 1st jump in the image from 1 to 2 (1803 AD to 1959 AD) then the 8th jump is between orbit 8 and 9 (2954 AD to 3120 AD)

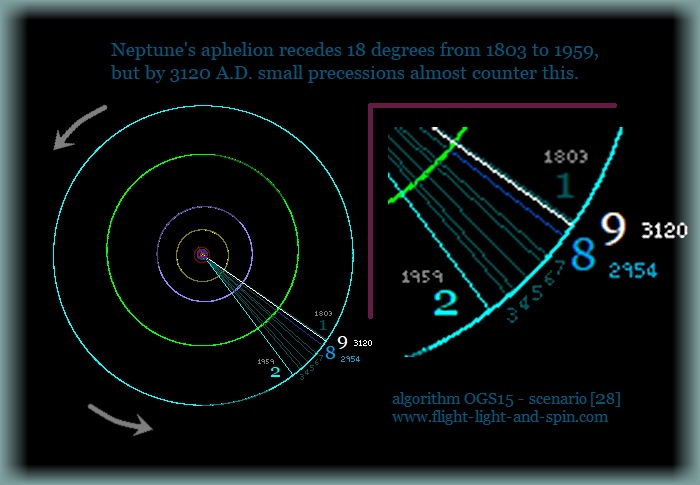
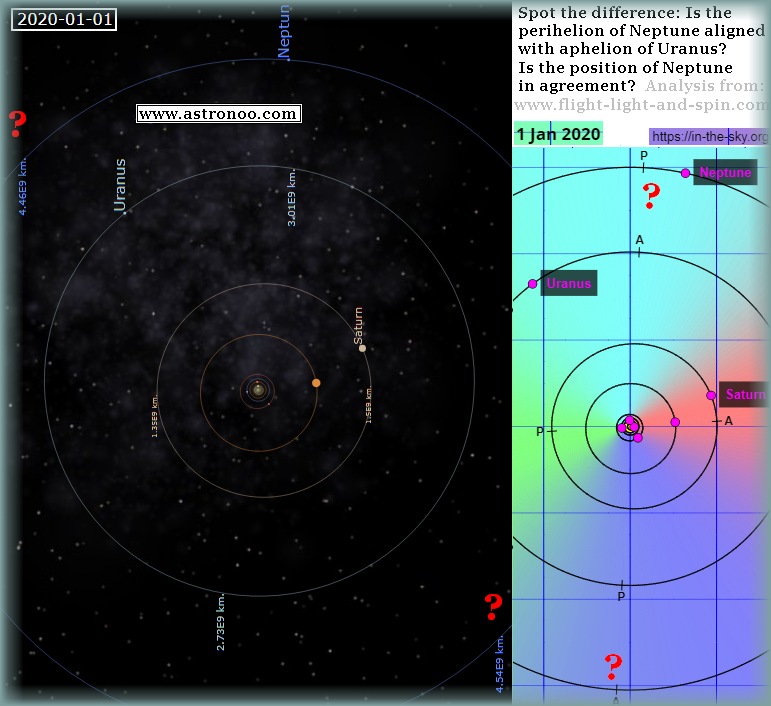
The large gray arrow indicates the direction of movement of the various planetary orbits. Now just compare this image to the images from the two websites at the top of this page. We can easily see how large the variation in the aphelion position is for Neptune. (Just note that you need to rotate the image around 180 degrees in your mind).

But it is abundantly clear just how vague the concept of an average is - unless you evolve an 3D-n-body algorithm, and then display a graph over many thousands of years.

Scenario [60] of OGS15 is a control test with just Neptune and the Sun. This is because OGS12 demonstrated that large time quanta will cause a recession to the major axis without any other planets effecting the orbit. So this scenario is required to show that this inaccuracy is only -0.0072 as/Ey when unaffected by other planetary gravity. So Scenario [60] should be compared to Scenario [28] in this regard as they both operate at 15000 virtual seconds per iteration.

I have not had the processing power to properly run Scenario [38], which will certainly calculate an error-margin 10x better, taking 10x longer at 1500 virtual seconds per iteration. If you have such power (or time), it would be fairly easy to run Scenario [38] of OGS15 to reveal a more accurate answer to Neptune's apparent recession to its aphelion and perihelion. I would be interested to know, and would be able to update my results accordingly. Though it may take a week or more to properly compute 25 orbits (or more!) of Neptune at this rate, as required.

If you do wish to partake in this free study, please contact me at the Cosmologos 21 forum here: cosmology.africamotion.net


Curiosity thou art a fiendish interloper into the complacent world of 'science'! When we examine the details in the Horizon Ephemeris, the only two perihelions vaguely applicable to Neptune are 1876-Aug-27 and 2042-Sep-04. And for a computer programmer, its a simple matter of applying the 'datediff' function which tells me those two dates are 60638 days apart. And with an orbit of 60189 days we have 449 days of Perihelion Precession. This is an arc-second difference of 9668 which is 58.7 as/Ey. Which makes the 0.36 as/Ey 'observation', (see Introduction) not just a joke, but a particularly unfunny one at that.

So let me now compare the Perihelion Precession of the Horizon Ephemeris to OGS15 for the orbit that will reach Perihelion more than 20 years from now.
.
2019/10/29 @ 02:58:52   OGS15   Version: 15.310 G=6.67259
[ 28 ] Neptune
15000 virtual seconds per calculation

Orbit # 2 sides to polygon = 346204
Aug/04/2042 perihelion   New Year: Apr/20/1942 12h33:00   aphelion Jul/06/1959
peri datediff = 60598    NY diff: 60105                   56956 = datediff aphe
min km 4447777308.43191                 |                 4539661807.29522 km max

Days/orbit =60104.861111111 days. +- .17361111 days AVG=60104.68750000
Year/orbit =164.555275759 years. +- .000475313 years AVG=164.554800446

THETA= 2.24289104217637 ==> NEW Min 4447777308.43191 @ 22h43:00
THETA= 5.35821650613247 ==> NEW Max 4539661807.29522 @ 02h43:00
AVG arcsec/yr PERI PREC = 66.3106 avg ERR(03.7435)
This orb=66.310566 arcsec/yr @ ind ERR(03.7435) & radian deviate 0.052902
.


So Horizon Ephemeris shows this orbit to advance by 58.7 as/Ey,
whereas OGS15 shows an advance of 66.31  (+-3.7)

Just for good measure, the next Perihelion Precession for Neptune was also measured.
By 2208-Aug-26 the yield was 58.5 as/Ey from Horizon Ephemeris data.
OGS15 results in 64.94 for that same orbit.

What's the point of this, you ask yourself?

Well the Relativists claim that the observation should be greater than the Newtonian prediction. But as I have clearly shown, the Newtonian value is in fact greater. I am only clear about one single fact. OGS15 is a perfectly accurate account of the Newtonian formula. That computer code has been offered as an act of good faith on my part on this page:
How to Build N-body-gravity Algorithm

There is zero room for significant error in the logic of the algorithm. It is an entirely transparent process with clearly defined error-margins within the computation.

If you note the graphs, we can see that those amounts were fairly close on an individual basis. But such large precessions must be countered by a radical recession to get anywhere near the averages claimed by utexas.edu (Introduction) and my own algorithm (OGS15 Download).

You may be asking yourself how it is that Neptune and Uranus were discovered if our understanding has so many holes in it. The answer is straightforward: The Astronomers of 1846 understood gravity better than the scientists of today.

In the next section we look at the general cycles of the planetary movements as dictated by the orbital dynamics between Saturn and Jupiter.


Sections of this Article by web-page


n-body gravity from www.flight-light-and-spin.com