The orbit of Mars is increasing its elliptical shape by over 500km per year. At its furthest distance, the aphelion of Mars is moving closer to Jupiter; whilst at its nearest, Mars' perihelion is moving closer to the Earth's orbit.

The data from NASA's Horizon Ephemeris (http://ssd.jpl.nasa.gov/horizons.cgi) follows. Each reading is the nearest and furthest that Mars is from the Sun in segments of 50 years. So the first reading shows the nearest and furthest from 1950-2000 A.D.

So how did I know that data was even there in the first place? Because my 2D algorithm OGS13 (orbit-gravity-sim-13.exe) had described very similar results. It has a function which records only changes to the most extreme orbits. The progression was quite easily detected. It was after noting this, that I went to check if the Jet Propulsion Laboratory had also expected such data. Well their database had done so, but I do not know if any person appreciates what the data is actually saying.

This phenomenon has thus been corroborated in an entirely blind study. So there is far more to the alorithms OGS13 and OGS15 (3D version) than deciphering the cause and nature of Perihelion Precession. There is another section that deals with the Perihelion Precession of: Mars. This here section is concerned with the distance of the Perihelion of Mars as it gets closer to the Earth.

The orbit of Mars fluctuates alot. In comparison with Horizon Ephmeris, the algorithm OGS15 (orbit-gravity-sim-15.exe) shows a similar but less average over 948 years from the perihelion of
:
Aug/04/1941 @ 206 592 353 km ---> 206 382 632 on Aug/01/2889.

Here Mars gets closer to Earth by -209 721 km or -221km per year. That data was Scenario [54] which calculates at 1500 seconds per quantum.

Notice that the date of those two dates are quite similar because they reflect a multiple of the 237 year cycle which resonates with all the major planetary influences on the orbit of Mars. If we use a 913 year sample, (perihelions Aug/04/1941 to Sep/22/2855) then the result is -225km per year that Mars gets nearer to us. Certainly the orbit of Mars is not stable, regardless of the sample or the algorithm.

The next table was generated at a less accurate rate of 15000 seconds per quantum. So each orbit is only a 3956 sided polygon. This was Scenario [64], but I increased the rate of computation to 15000 seconds per quanta, so it may lack some accuracy. I then simply extracted the perihelion such as to optimize it for the movements of the other planets. Note the rate of change of the orbit #.

In the column 'orbit dif per year' I measure the difference between individual perihelions and the picture looks quite astonishing. The rate of closure gets more extreme by 1km every 80 years. In 80 000 years time, that will be over 1200km per year as a rate of closure. That is over 700km per year as an average rate of approach. The total amount of closure is then 56 million km.

Thus Mars will have already assaulted the Earth in less than 80 millenia. Of course that rate is likely to have a subtle rate of change, and I am just drawing a straight line where the line is not actually straight. But it looks to me as a rule of thumb that the extreme scenario is going to win. In the section Newtonian-Planck Gravity i investigate this dynamic in the context of all the planets, and there you will find further evidence against a stabilizing Martian orbit.

Table A is extracted data that reflects the perihelion of individual orbits in the cycles that balance the effects of the planets to avoid atypical movements. So that is why the orbit count is in proportions quantified by 126 orbit cycles. The first two rows (1 & 63) are less than the 126 orbit cycle, so that detail has been omitted; but they have been included simply as points of reference.

The next graph is in cycles of 1826 years. It might thus be more accurate. The Scenario runs from a start of 1773 AD:

Here I use Scenario [82] which isolates the extremity of perihelion, recording the exact detail whenever a new lowest distance is reached. I then select the first extremity after every 971 orbits, or 1826 years.

The aphelion matched this movement almost exactly with increases in distance also diminshing at the overall rate of 58 km over the 11 thousand years from the 39th century AD to the 149th AD. Which is 1km every 190 years that the rate of increasing eccentricity diminshes.

I have to then draw a straight line from here and suggest that 143 x 190 = 27 thousand years after the year 14812 AD, that Mars' will cease to become increasingly eccentric. Will it stay in that shape or begin to circularise again? I do not know! Yet.

But after 42 thousand years of such a process the orbit will have closed in on the Earth by 4 million kilometers. So despite all this number crunching I am still uncertain what the outcome will be.

And it is vital to appreciate that the algorithms OGS13 and OGS15 are simply part of the Newtonian paradigm. These algorithms examine all the gravitational effects that the 9 primary bodies of the solar system have on one another (8 major planets and the Sun). They have absolutely nothing to do with any post-Newtonian theories on gravity, physics, or geometry. Euclid, Newton and Plank's quantum time are all that is required to have this effect.

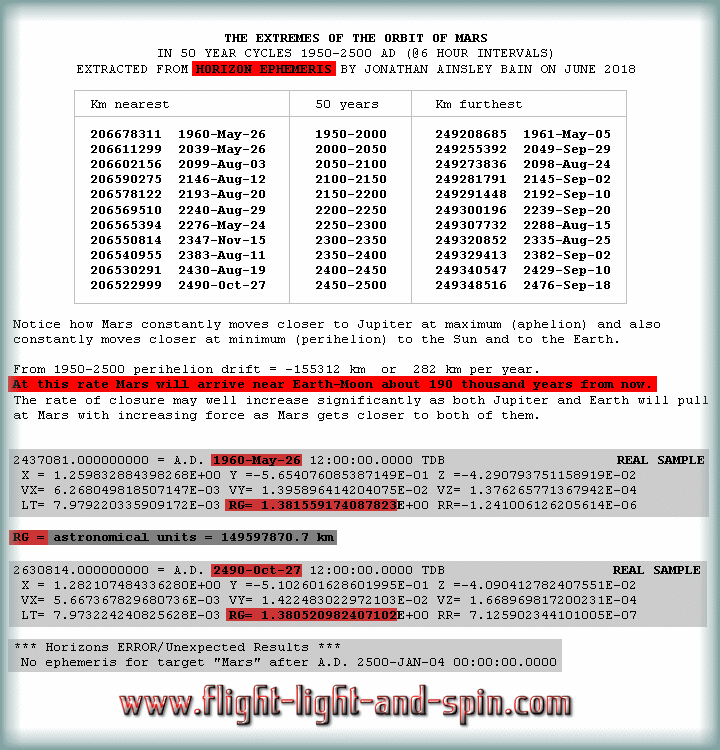
But what about the data from Horizon Ephemeris? They claim vague Relativistic influence, but they do not offer a transparent description of their processes or theories on gravity. Its seems their method is statistical, and not rigorous application of the laws of any particular theory on gravity itself. For no apparent reason they do not venture beyond 2500 AD for Mars. Although they do go beyond this date for all the other planets. Perhaps they have noticed the weirdness of the Martian orbit, and are unsure how to proceed with the data. My algorithm can take it further, but I lack the processing power as I am simply using an entry level 1.5 GHz laptop.

If you have good processing power, you can partake in this study quite easily by simply download OGS15 and clicking scenario [81] or [80]. The time it takes to evolve beyond 2500 AD will vary considerably depending on your computer. Scenario [81] evolves at 1500 seconds per quanta of time, which is 10 times more accurate than Scenario [82] which is the table above. Whereas Scenario [80] runs at just 15 seconds per quanta of time. It is thus 100 times slower, but an evolution 100 time more accurate.

Should you decide to do this, first read about the algorithm on this page: Orrery
Download the software itself here: Download
Post your results that will be generated into the data-drift.txt file on the following forum:
http://www.cosmology.africamotion.net/f6-computer-algorithms

Alternatively, you may want to build a 3d-n-body algorithm yourself. My formula is freely available, as well as selected extracted planetary data, here:
How to Build N-body-gravity Algorithm

Nevertheless it is the orbit of Mars that is by far the most fascinating in terms of 3d-n-body-gravity, because this orbit is extensively altered by the gravity of Jupiter, as well as by the lesser gravity of the Earth. It is not just that Jupiter is pulling Mars towards it by over 200km per year, but also that as a result of this pull, the perihelion of Mars' orbit is moving closer to the Earth.

The orbit of Mars is becoming increasingly eccentric because of the gravity of Jupiter (90%) and the Earth (10%). But the Earth is much closer to Mars than Jupiter is. So the Earth's gravitational effect on Mars will have an increasing proportion of the total effect the closer it gets to us. So Mars could reach Earth before it becomes a moon of Jupiter... if this dynamic persists.

If it continues like Table A , it would mean that the orbit of Mars is going to intersect with the orbit of the Earth and the Moon, within 80 thousand years! Perhaps alot less time than this if the rate increases significantly due to the increasing effect of the Earth's gravity. Mars and the Earth could be about to have a gravitational tug-of-war over the Moon. The outcome of that is beyond this particular study with potential results being: Collisions between any of the three bodies; or perhaps Mars actually stealing the moon from the Earth; or even Mars becoming a second moon of Earth.

Surely this sounds far-fetched, the stuff of sci-fi? Its not. This started as an analysis of the famous Perihelion Precession of Mercury. But the orbit of Mars is far more curious. If you go to Horizon Ephemeris you will see that it defaults to the orbit of Mars. That s no coincidence. Martian invasion takes on a whole new meaning.

Later on I'll show you how to extract such data from NASA's Jet Propulsion Laboratory's Horizon Ephemeris databases yourself. Put your doubt where your time is, or start packing your bags for departure to Ganymede, because Horizon's data clearly shows Mars moving towards the Earth at over 250km per year! How could Mars have gotten into such a predicament? I deal with that later in the section:
Newtonian-Planck Gravity

<— Page Back — Start Page — Next Page —>